Ένας ακόμα σύνδεσμος

http://www.miqel.com/fractals_math_patterns/visual-math-phi-golden.html

Δείτε τις εικόνες της ιστοσελίδας και επιλέξτε αυτές που είναι σχετικές με το αντικείμενο της έρευνας σας.

Ο ναυτίλος

Ο ναυτίλος είναι ένα ζωντανό απολίθωμα που επιβίωσε στους ωκεανούς για πάνω από 500 εκατομμύρια χρόνια. Υπάρχει πριν από τα ψάρια, τους δεινόσαυρους και τα θηλαστικά! Ο Ναυτίλος μπορούσε να φτάσει μέχρι τα 6 μέτρα μήκος και ήταν αρπακτικό στις αρχαίες θάλασσες.   Σας θυμίζει κάτι;;;
 

Οστρακα, κυκλώνες, γαλαξίες και χρυσή τομή

Τόσο η φύση όσο και οι καλλιτέχνες φαίνεται ότι ακολουθούν τους κανόνες της αρμονίας, η οποία βασίζεται σε μαθηματικούς τύπους που είχαν επινοήσει οι αρχαίοι Ελληνες

H λογαριθμική σπείρα (με μπλε γραμμή) μπορεί να εγγραφεί σε μια άπειρη ακολουθία «χρυσών» ορθογωνίων (με κόκκινη γραμμή)

Ο Πυθαγόρας υποστήριζε ότι αποτελεί μια από τις κρυμμένες αρμονίες της φύσης. Ο Ικτίνος τη χρησιμοποίησε στην κατασκευή του Παρθενώνα και ο Ντα Βίντσι στα υπέροχα γυμνά του. Κανένας όμως δεν μπορούσε να φανταστεί ότι χαρακτηρίζει τη μορφή φυσικών σχηματισμών σε όλες τις κλίμακες των μεγεθών, από τις μικρότερες, όπως είναι τα όστρακα, ως τις μεγαλύτερες, όπως είναι οι κυκλώνες και οι γαλαξίες. Πρόκειται για τη Χρυσή Τομή.

Υπολογισμός του Χρυσού Αριθμού Φ - Μαθηματική προσέγγιση (ii)

Ας προσπαθήσουμε να προσεγγίσουμε ΜΑΘΗΜΑΤΙΚΑ τον ΧΡΥΣΟ ΑΡΙΘΜΟ και να δούμε κάποιες ΜΑΘΗΜΑΤΙΚΕΣ εφαρμογές του .

Α. ΕΙΣΑΓΩΓΗ ΣΤΟ ΠΡΟΒΛΗΜΑ ΤΗΣ ΧΡΥΣΗΣ ΤΟΜΗΣ :

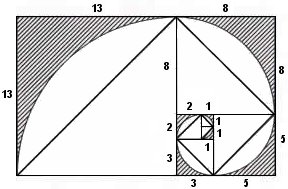
Στο σχήμα 1 έχουμε το ευθύγραμμο τμήμα ΑΒ . Εστω Γ είναι το σημείο που διαιρεί σε "χρυσή τομή" το ΑΒ . εάν ορίσουμε το ΑΒ = α και ΑΓ = χ τότε θα έχουμε :
==> AB / AΓ = ΑΓ / ΒΓ ή α / χ = χ / (α-χ)
Από την σχέση αυτή προκύπτει η δευτεροβάθμια εξίσωση
χ2 (χ στο τετράγωνο) + αχ - α2 (α στο τετράγωνο) = 0 .
Από την οποία βρίσκουμε την τιμή της χ (=ΑΓ) , πραγματικά έχουμε ...
χ(χ+α) = α2 (α στο τετράγωνο) .... που σημαίνει ότι. ...
Το άγνωστο τμήμα χ (ΑΓ) είναι η μικρότερη πλευρά ενός ορθογώνιου παραλληλογράμμου , το οποίο είναι ισοδύναμο με τετράγωνο πλευράς α (ΑΒ) και του οποίου (ορθογωνίου) οι διαστάσεις (πλευρές) διαφέρουν κατά α .